Eine „Carrollsche“ Tafel

Die 6 Full-Contact -Zigaretten der letzten Woche können mit der in der Abbildung gezeigten Anordnung verbessert werden, bei der eine siebte Zigarette in eine zentrale Vertiefung gesteckt wird, die durch die anderen gebildet wird.

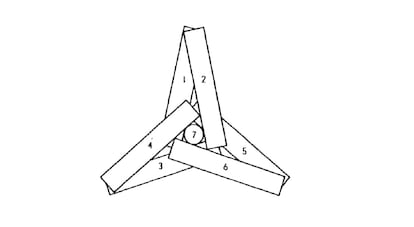
Was (soweit ich weiß) nicht bewiesen wurde, ist, dass 7 das Maximum ist (obwohl bewiesen wurde, dass die Lösung der Abbildung nicht eindeutig ist, wie wir später sehen werden).

Was Zigaretten – oder Zylinder – mit unendlicher Länge betrifft (die Variante wurde vom britischen Mathematiker John Littlewood vorgeschlagen), so haben sie die Aufmerksamkeit meiner aufmerksamen Leser nicht verdient, da sie keine Lösung boten. Obwohl es vielleicht keine Frage der Aufmerksamkeit war, sondern der Schwierigkeit, denn man muss zugeben, dass es alles andere als einfach ist : Die Abbildung zeigt eine Lösung mit 6 Zylindern, die bis vor kurzem als unüberwindbar galt. Es wurden zwei verschiedene Lösungen mit 7 Zylindern gefunden (was offensichtlich auch bei endlichen Zigaretten der Fall ist). Wenn Sie sich die Abbildung genau ansehen und von ihr ausgehen, finden Sie möglicherweise eine dieser Lösungen. Aber wappnen Sie sich mit Geduld, denn obwohl das Wissen um seine Existenz die Dinge einfacher macht, ist es dennoch sehr schwierig.

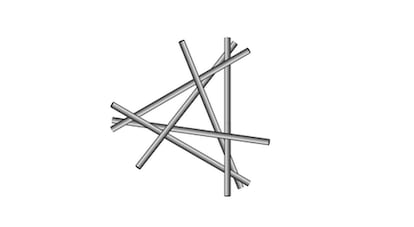
Und der Übergang von starren zu flexiblen Zylindern ist ein einfaches Problem, um die Schwierigkeiten der vorherigen auszugleichen:

Wir haben ein 1 Meter langes Gummiband mit einem kreisförmigen Abschnitt von 2 mm Durchmesser. Wenn wir es dehnen, bis sein Querschnitt 1 mm im Durchmesser beträgt, und davon ausgehen, dass die Verformung über die gesamte Länge des Gummis gleichmäßig ist, wie lang ist es dann? Und wenn Sie die Lösung gefunden haben, versuchen Sie, sie zu „kochen“.

Die Beziehung zwischen Dehnung und Schrumpfung wird als Poissonzahl bezeichnet und ist bei den meisten Materialien positiv (je größer die Dehnung, desto größer die Schrumpfung). Manche Materialien, sogenannte auxetische, weisen jedoch eine negative Poissonzahl auf, was bedeutet, dass sie sich bei Dehnung ausdehnen.

Synthetische auxetische Materialien wie expandiertes Polytetrafluorethylen (das unter anderem unter dem Namen Gore-Tex vertrieben wird) haben viele Anwendungsmöglichkeiten. Und zufälligerweise (obwohl in der Mathematik und der makroskopischen Physik nichts zufällig ist) ist eine maximale Anzahl von Fäden (in der Praxis unendliche Zylinder), die sich gegenseitig berühren, die Grundlage für die Herstellung auxetischer Netze. Dies veranlasste die Forscher, nach diesem möglichen Maximum zu suchen. Wie sie vor den Mathematikern herausfanden, war es 7.

Eine nichteuklidische Tafel?

Die beiden Mädchen in der Hauptabbildung der letzten Woche scheinen nicht besonders gut in Mathe zu sein, wenn man nach dem geht, was sie an die Tafel geschrieben haben. Aber urteilen wir nicht zu schnell: Sie mögen in unkonventionellen Worten ausgedrückt sein, aber das bedeutet nicht, dass sie falsch sind. Oder vielleicht waren sie Gegenstand eines mathematischen Witzes, den sich Lewis Carroll selbst ausgedacht hat, der junge Mädchen so gerne mit seinem offensichtlichen Unsinn verwirrt. Besteht die Möglichkeit, dass die Gleichheit 180 = 90 + 30 Sinn ergibt?

Andererseits addieren sich die Winkel eines Dreiecks in der euklidischen Ebene nur zu 180º; auf einer anderen Oberfläche können sie mehr oder weniger als zwei rechte Winkel ergeben (können Sie ein Dreieck zeichnen – oder beschreiben –, dessen Winkel zusammen 270º ergeben?).

Was das Dreieck auf der Tafel betrifft, wissen wir, dass es rechtwinklig ist, weil wir die übliche Markierung des verborgenen Winkels sehen, jedoch nicht seinen Wert (nur die letzte 0 ist sichtbar). aber wir sehen den Wert der Höhen: 40º bzw. 30º. Ist es möglich, dem verdeckten rechten Winkel einen Wert zuzuweisen, der der Figur einen Sinn gibt?

Und von der Illustration der letzten Woche können wir zum Text übergehen, um ein kleines Metaproblem zu stellen: Welchen logischen Grund könnte es dafür geben, dass die automatische Rechtschreibprüfung den Namen Poisson, des berühmten französischen Mathematikers und Physikers, kursiv schreibt?